【数学II】微分法の基礎

問答庫　　理数　　数学

【数学II】微分法の基礎の解説

2020.11.20

FmM7

問答庫プログラム担当です。記事は主に問答校を担当します。音楽理論にはまってます。

詳しく見る

数学Ⅱ 微分

お気に入りに追加

問答庫塾
生徒募集中！

数IIの強大な壁、微分を書き手の復習を兼ねて解説します。技術テスト的側面も強いので参考程度に見ていただければと思います。また、以下で使用しているグラフに関してはこちらのリンク からアクセスできます。参考資料としてご覧ください。

重要語句を隠す

1. 微分とは

2. 微分係数の問題

3. 導関数の問題

微分とは

そもそも微分とは、簡単に言ってしまえば「関数上のある点における接線の傾き」のことです。例を見てみましょう。まず

f (x) = \frac{x^{2}}{8}

となる関数f(x)を定義し、関数f(x)上にP(p, f(p))を取ります。ここではP(2, 0.5)とします。更にこの点における接線P´を取りたいと考えます。(名前が違いますが下画像の赤線です)

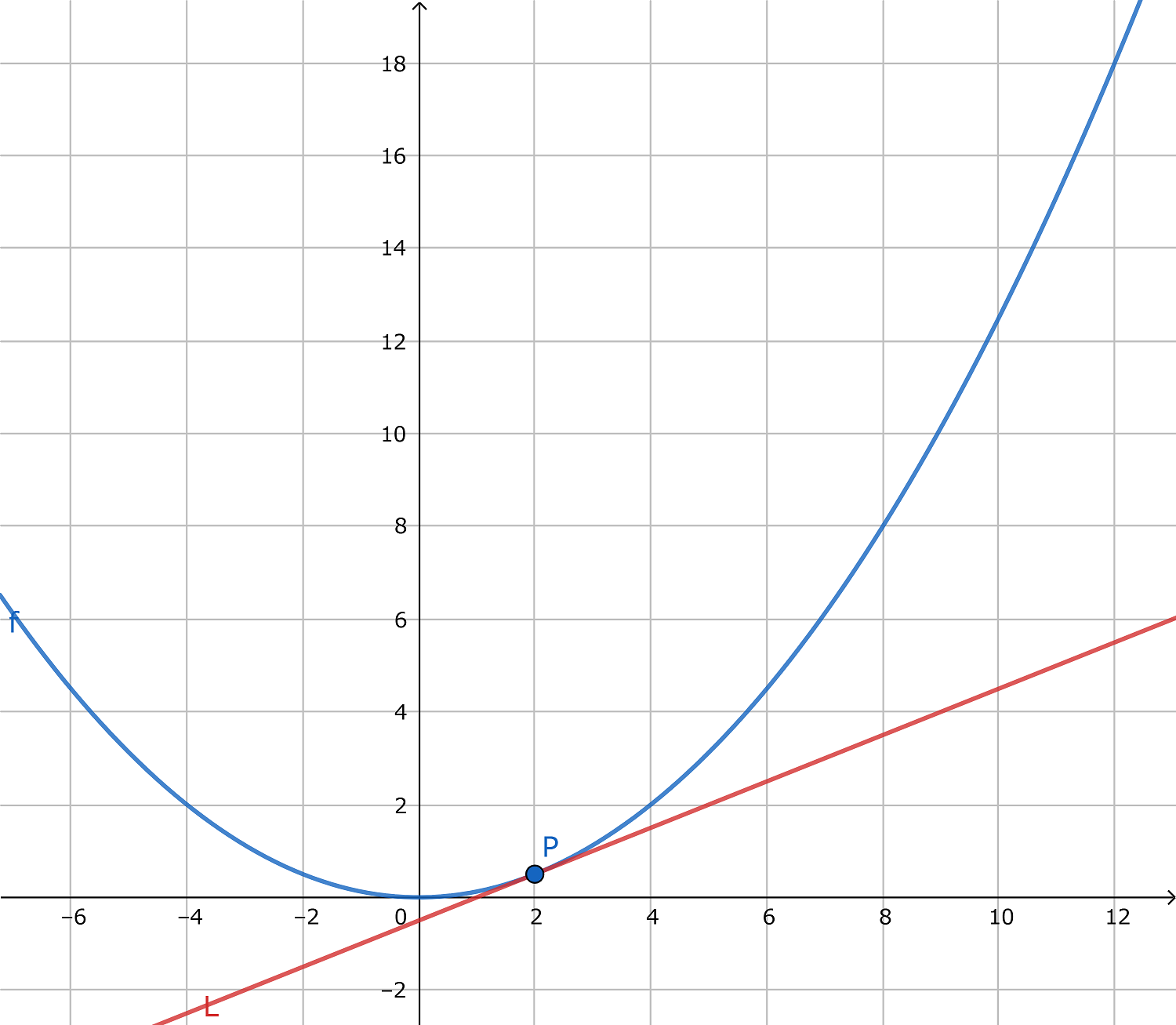
方法として考えられるのは判別式を用いることですが、3次関数などへの拡張性が低いためあまり良くありません。これを解くため、ここでf(x)上のPでない点Q(q, f(q))を取り、直線PQについて考えてみます。(ここではQ(10, 12.5)ですがP≠Qであればよいです)

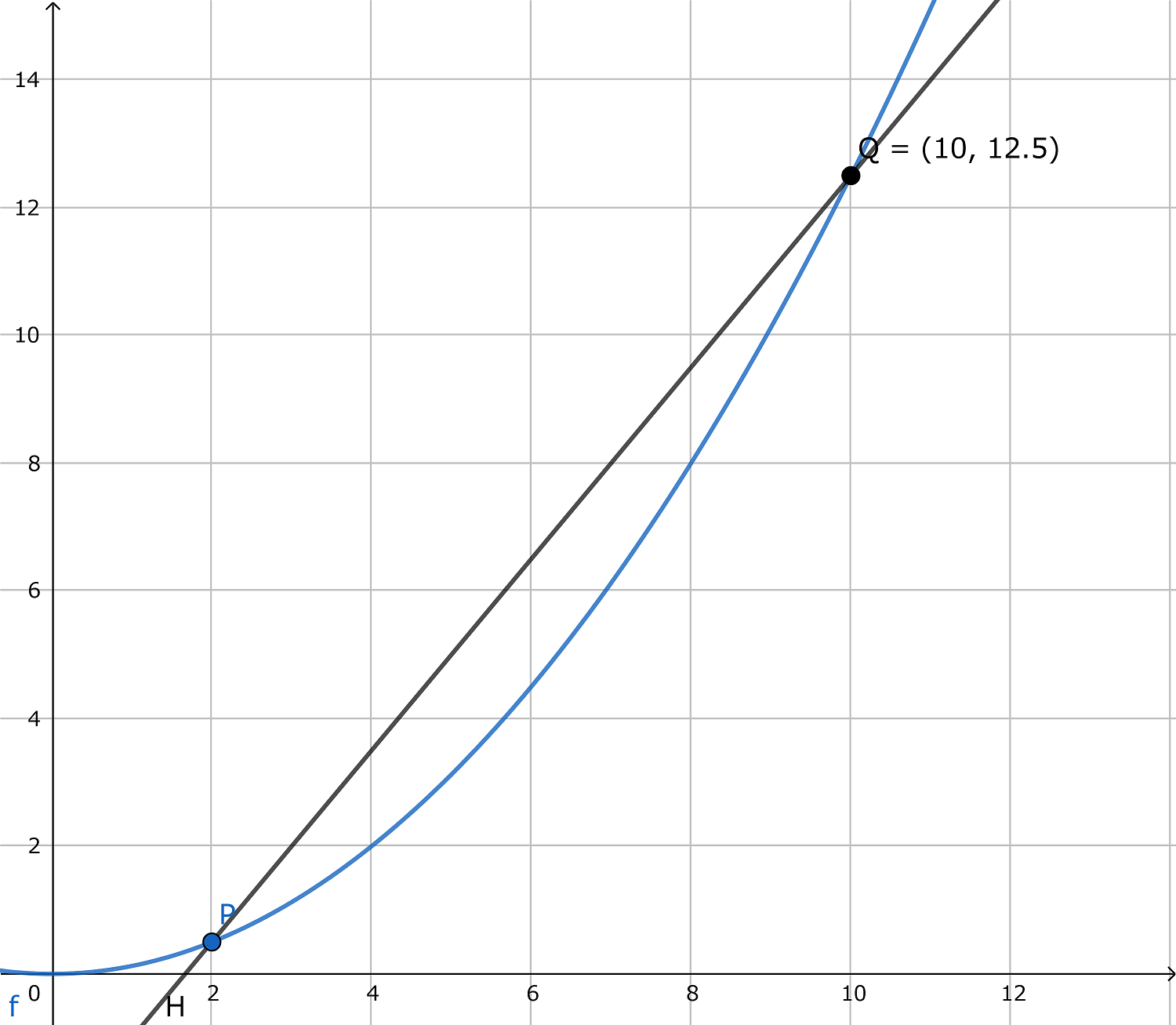
ここで、qを変化させてpに近づけていくと、PQが徐々にPにおける接線に近づいていきます。(下画像参照)

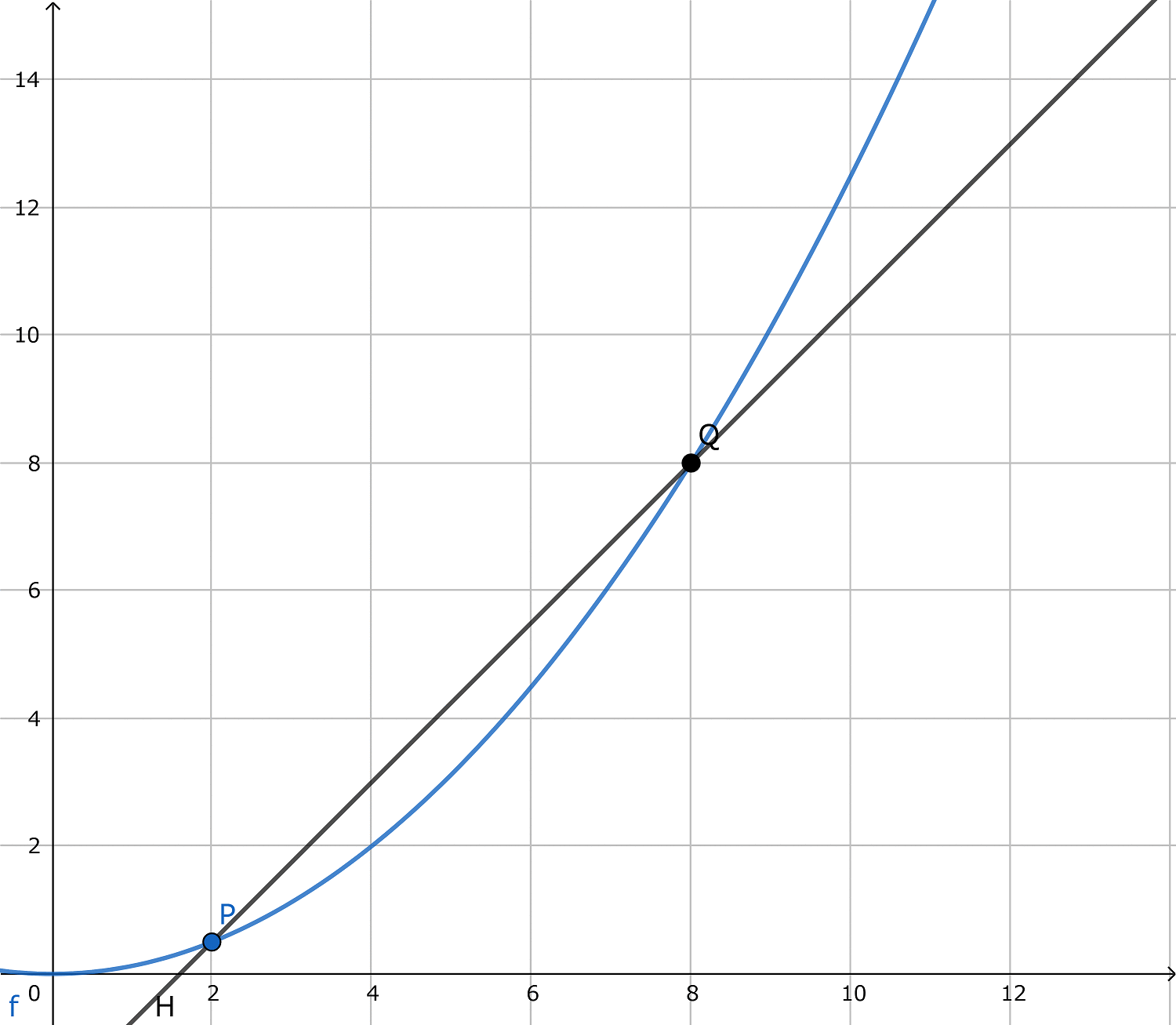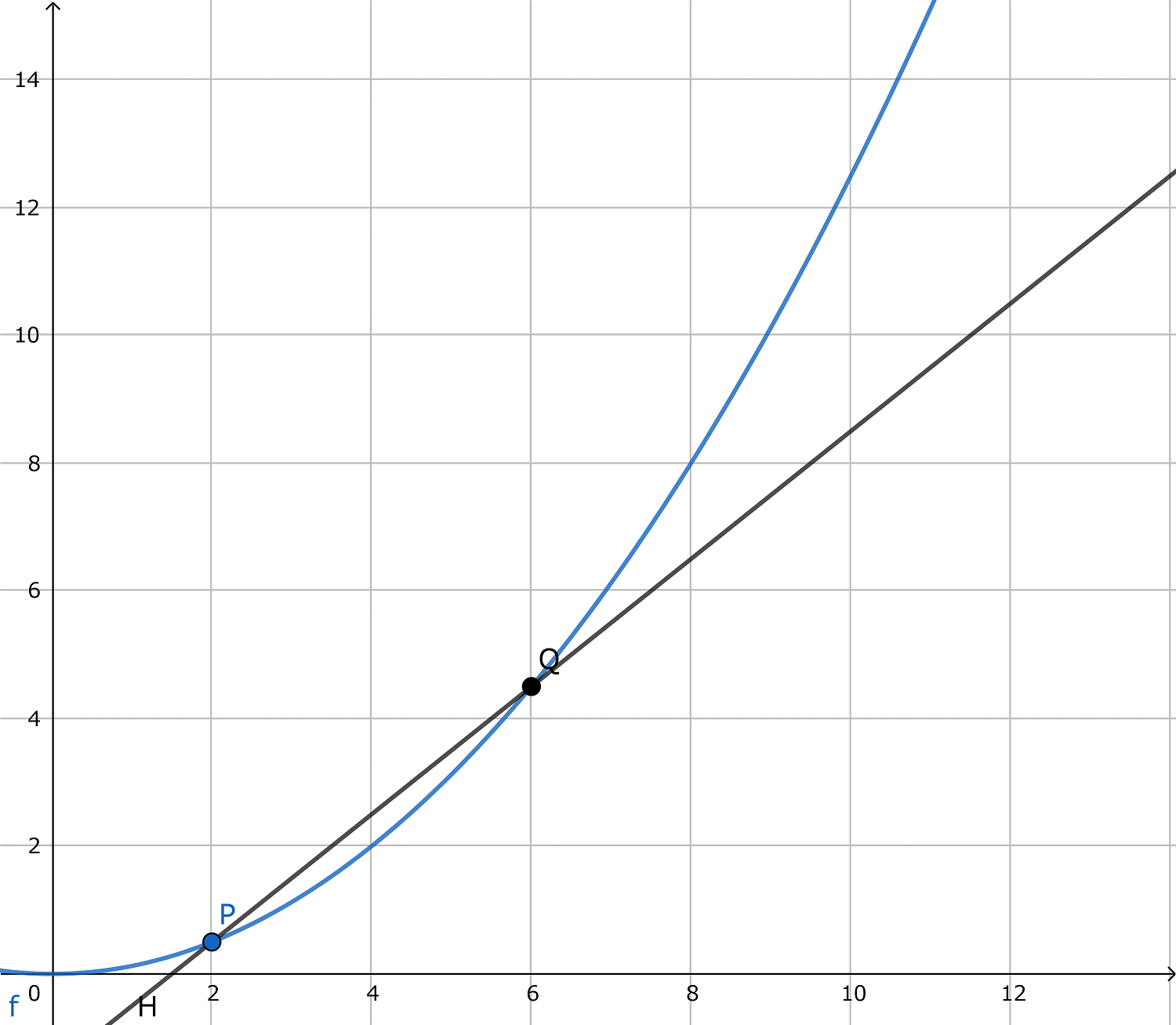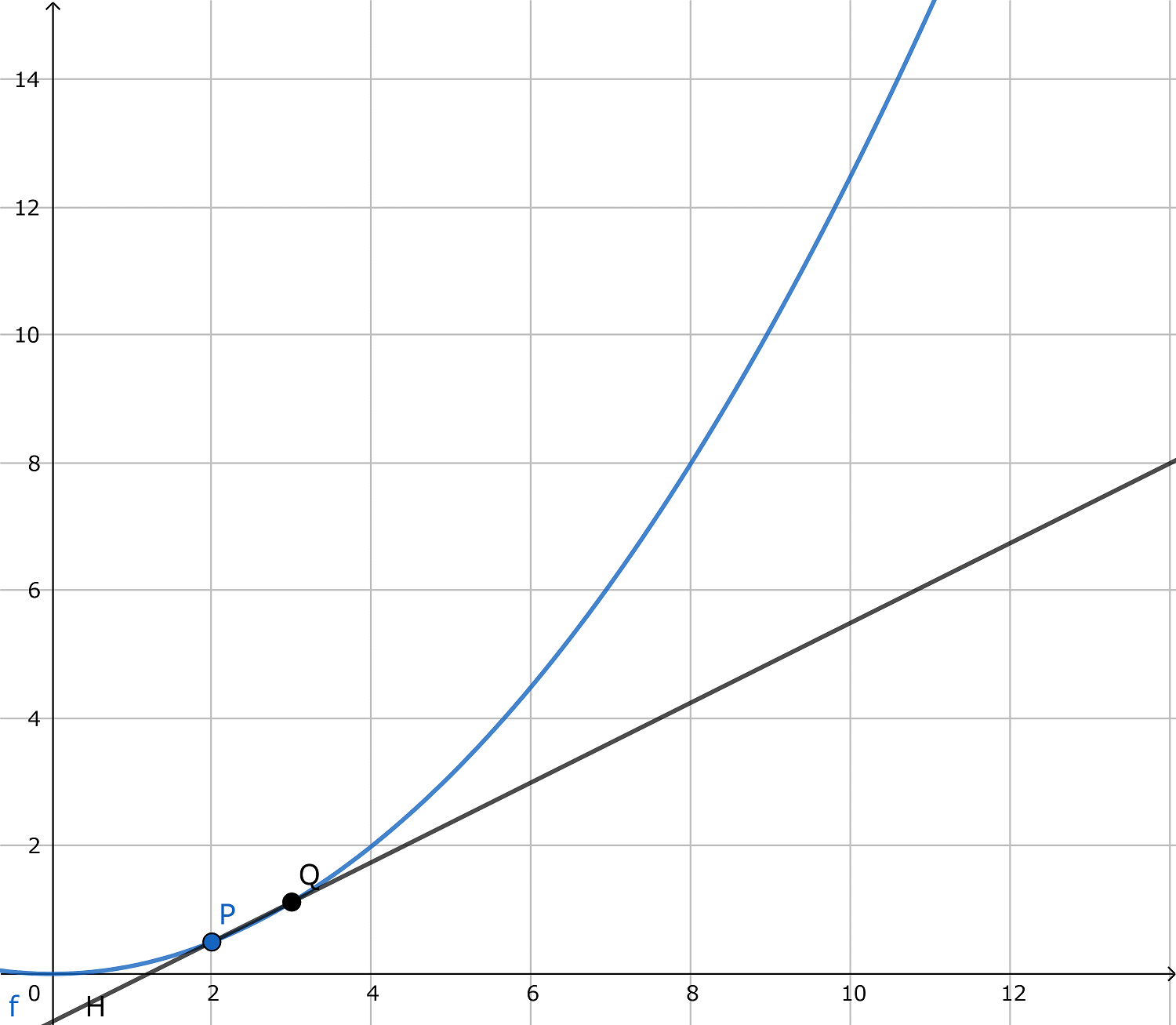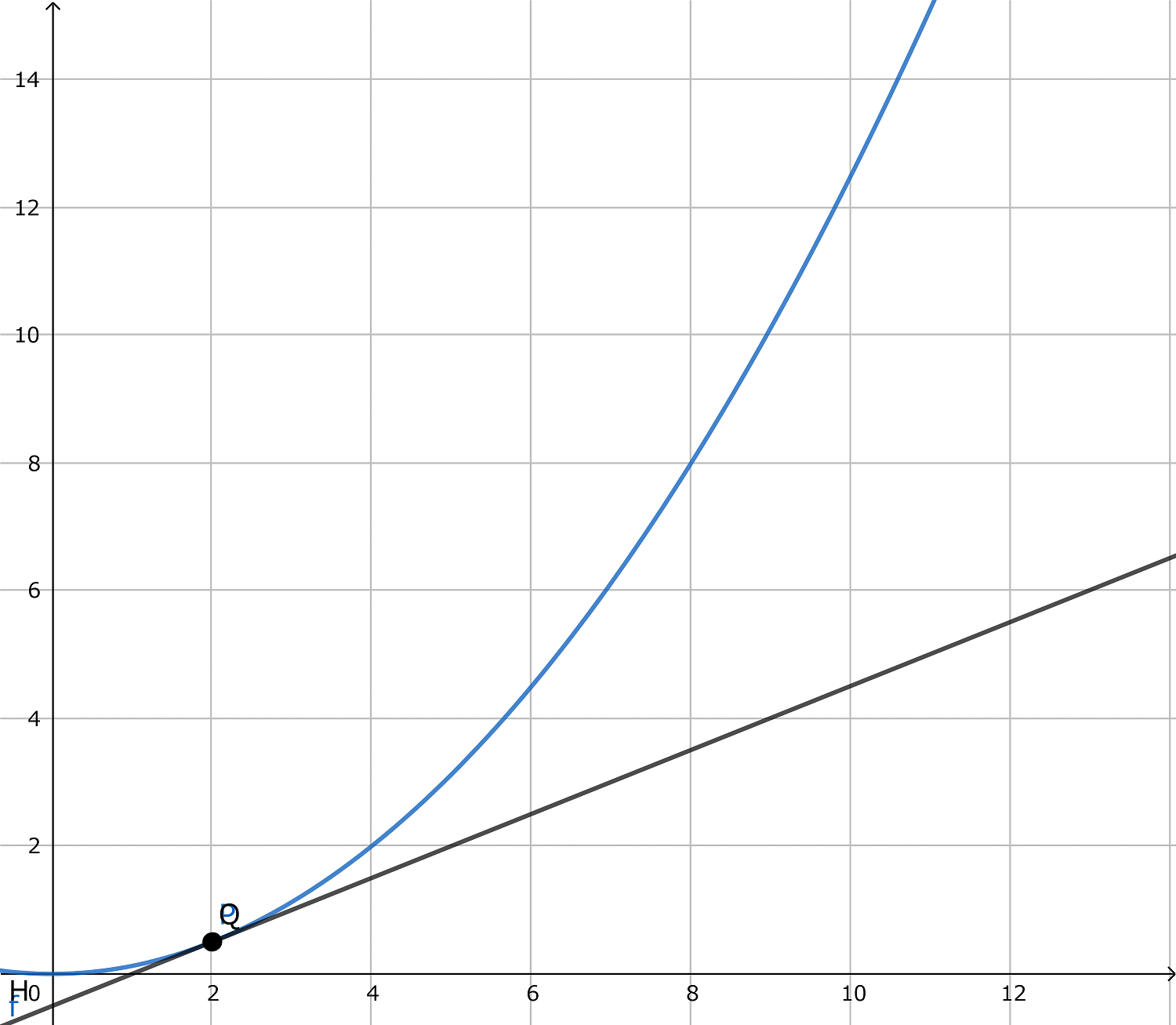
じゃあq=pにしてしまえばいいじゃないか、という話ですが、これはPQの式を立式するとわかります。

(a,b)を通る傾きcの一次関数はy-b=c(x-a)とあらわすことができるので、直線PQに関しても同様のことが言えます。まずP(p,f(p))を通るのでy=c(x-p)+f(p)とできます。また、傾きは(y座標の差)÷(x座標の差)で求めることができるので、PQは以下のようになります。

PQ: y = \frac{f (q) - f (p)}{q - p} (x - p) + f (p)

上記のPQの式を見ると分かる通り、q=pの時q-p=0となり、分母が0になってしまうのでp≠qでなければなりません。ここで、「qを限りなくpに近づける」という概念を取り入れます。これは極限というもので、limという記号が用いられます。まず実際にこれを用いて先ほどのPQ改めP´の方程式を立式してみます。

P´: y = \lim_{q \to p} {\frac{f (q) - f (p)}{q - p} (x - p) + f (p)}

いきなり意味が分からなくなりましたが、この式の展開はシンプルです。まず、limの対象(この場合{}の内側)となる部分を整理して(この場合特に分母のq-pを処理する)qにpを代入するだけです。

極限に近づけるだけなのに代入していいのか？というところですが、深く考えなくて大丈夫です。 (一応、極限に近づけた値は代入しても近づけられた値での計算と結果が変わらない、ということがあります。 1/3=0.333･･･を3倍すると1に極限まで近づいた0.999･･･となり、1として扱われることと同じです。)

では早速P´の展開をしていきましょう。

P´: y = \lim_{q \to p} {\frac{f (q) - f (p)}{q - p} (x - p) + f (p)}

= \lim_{q \to p} {\frac{\frac{q^{2}}{8} - \frac{p^{2}}{8}}{q - p} (x - p) + \frac{p^{2}}{8}}

= \lim_{q \to p} {\frac{\frac{1}{8} (q + p) (q - p)}{q - p} (x - p) + \frac{p^{2}}{8}}

= \lim_{q \to p} {\frac{q + p}{8} (x - p) + \frac{p^{2}}{8}}

= \frac{p}{4} (x - p) + \frac{p^{2}}{8}

= \frac{p}{4} x - \frac{p^{2}}{8}

実際にP´が接線となるかグラフ上で確かめてみましょう。

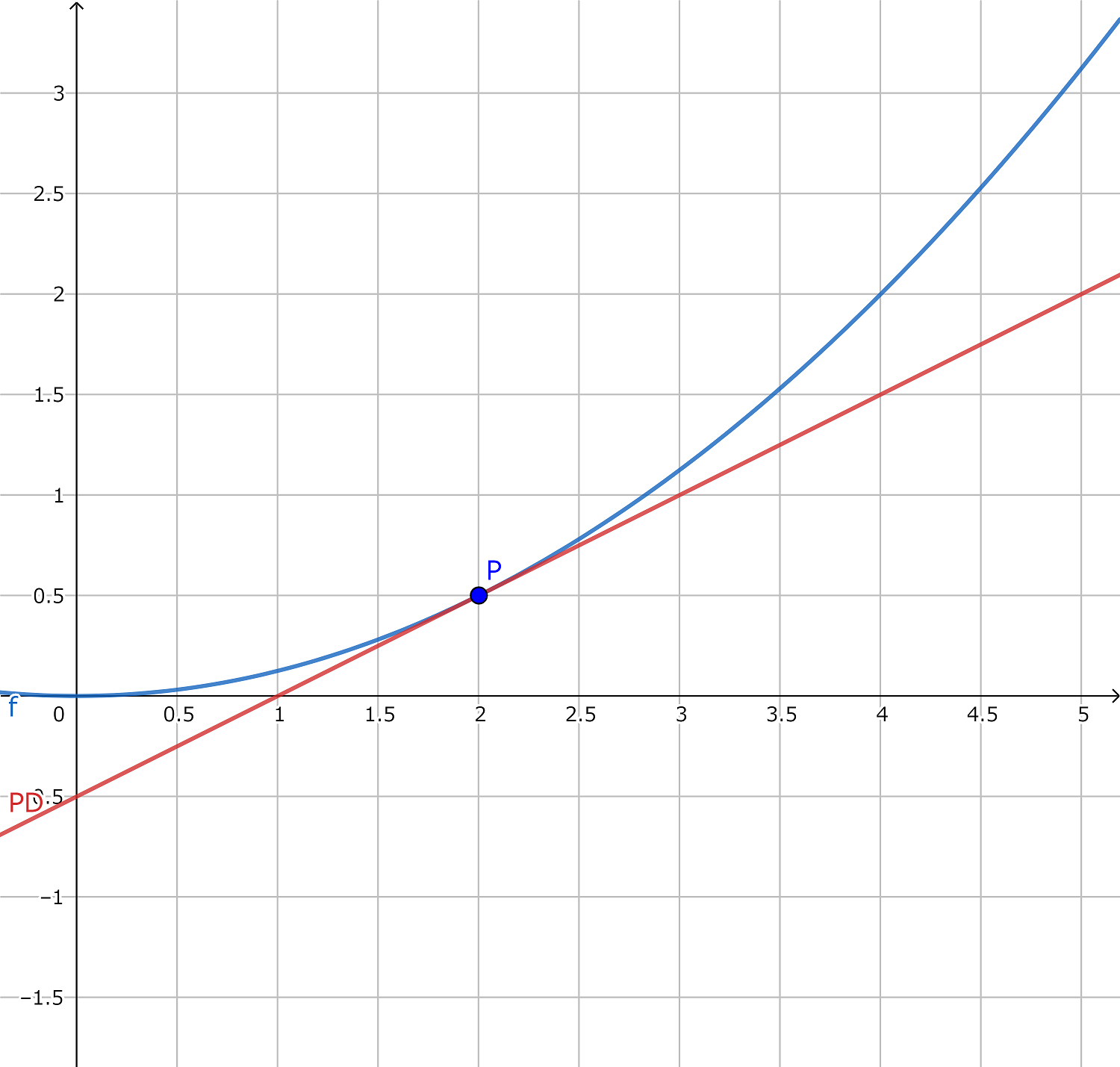
最初なので、一応f(x)とP´の計算でも確かめてみます。

f (x) = \frac{x^{2}}{8}

P´ = \frac{p}{4} x - \frac{p^{2}}{8}

= \frac{1}{2} x - \frac{1}{2}

f (x) - P´

= \frac{x^{2}}{8} - \frac{1}{2} x + \frac{1}{2} = 0

これを解いて

x^{2} - 4 x + 4

= {(x - 2)}^{2} = 0

以上より、f(x)とP´の接点がx=2の点(この時はP)のみであり、P´がPにおけるf(x)の接線であることがわかりました。

このように、関数上のある点の傾きの事を微分係数といいます。特に今回はPについて考えたので、 P´の傾きはf(x)のx=pにおける微分係数といえます。
また、Pにおける微分係数をf´(p)と表します。 $(\frac{d}{d x} f (x) や、$ $\frac{d y}{d x} と$ $表記することもあります。)$ ではここで定数aに関してf´(a)の定義を見てみましょう。

f ´ (a)

= \lim_{b \to a} \frac{f (b) - f (a)}{b - a}

(a \neq b)

または

f ´ (a)

= \lim_{h \to 0} \frac{f (a + h) - f (a)}{h}

(h \neq 0)

前者は先ほど見たものと同じですが、後者は見覚えがない形です。ではここで前者の式を変形して後者の式を導き出しましょう。
まずh=b-aと置きます。(これが全てですが)

f ´ (a) = \lim_{b \to a} \frac{f (b) - f (a)}{b - a}

= \lim_{b - a \to 0} \frac{f (a + (b - a)) - f (a)}{b - a}

(a \neq b)

= \lim_{h \to 0} \frac{f (a + h) - f (a)}{h}

(h \neq 0)

一応こう書きましたが、本質的なことはbをaではないx座標としてではなく、0ではないhだけ移動したaとして見ている、ということです。つまり二点の存在ではなく二点の差に着目している、ということです。
なお、今後この式を使うときは大抵hを用いた方が使われます。(使うことは少なくなりますが...)

また、ここで定数aではなく変数xに関してこの式を置くと、

f ´ (x)

= \lim_{h \to 0} \frac{f (x + h) - f (x)}{h} (h \neq 0)

となります。この式の事をf(x)の導関数と呼び、この導関数を求めることを微分するといいます。

微分係数の問題

では実際に解いてみましょう。とはいえ先程と内容はほとんど変わりません。まず一つ例題とその解法を示します。

例1

f (x) = x^{2} + 2 x

について、

x = 3

における微分係数を求めよ

では解いていきます。先ほどの公式をf(3)に置き換えて展開していくだけです。

f ´ (3) = \lim_{h \to 0} \frac{f (3 + h) - f (3)}{h}

= \lim_{h \to 0} \frac{{(3 + h)}^{2} + 2 (3 + h) - (3^{2} + 2 \times 3)}{h}

= \lim_{h \to 0} \frac{h^{2} + 8 h}{h}

= \lim_{h \to 0} (h + 8) = 8

この通り、非常に簡単にできます。

ここからは練習問題とその解説です。是非紙とペンを手に取って一度解いてみてください。

問1

次の f (x) について、

x = 2 における

微分係数を求めよ

(1) f (x) = 3 x - 5

(2) f (x) = x^{2} - 4 x - 5

解説は以下の通りです。(ボタンを押すと解説が展開されます。)

展開する

まず(1)です。とりあえず公式を用いて展開しましょう。

f ´ (2) = \lim_{h \to 0} \frac{f (2 + h) - f (2)}{h}

= \lim_{h \to 0} \frac{{3 (2 + h) - 5} - (3 \times 2 - 5)}{h}

= \lim_{h \to 0} \frac{3 h}{h} = 3

考えれば当然ですが、3x-5は直線なのでどの点でも微分係数は3で一定です。

続いて(2)です。これもとりあえず公式を用いて展開しましょう。

f ´ (2) = \lim_{h \to 0} \frac{f (2 + h) - f (2)}{h}

= \lim_{h \to 0} \frac{{{(2 + h)}^{2} - 4 (2 + h) - 5} - (2^{2} - 4 \times 2 - 5)}{h}

= \lim_{h \to 0} \frac{h^{2}}{h} = 0

この場合、0が解とはどういうことでしょうか。傾きが0ですから、接線を取るとy座標が一定の定数関数となります。(下画像参照)

ちなみにこのグラフはこちらのリンクから見ることができます。

導関数の問題

例2

f (x) = {2 x}^{2} + 5 x - 6

を微分せよ

では解いていきます。こちらも公式を使うだけです。

f ´ (x)

= \lim_{h \to 0} \frac{f (x + h) - f (x)}{h}

= \lim_{h \to 0} \frac{2 (x^{2} + 2 x h + h^{2}) + 5 (x + h) - 6 - ({2 x}^{2} + 5 x - 6)}{h}

= \lim_{h \to 0} \frac{(4 x + 5) h + 2 h^{2}}{h}

= 4 x + 5

問2

以下の f (x)

を微分せよ

(1) f (x)

= - x^{2} + 8

(2) f (x)

= x^{3}

解説は以下の通りです。(ボタンを押すと解説が展開されます。)

展開する

まず(1)です。公式で展開します。

f ´ (x) = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h}

= \lim_{h \to 0} \frac{- (x^{2} + 2 x h + h^{2}) + 8 - (- x^{2} + 8)}{h}

= \lim_{h \to 0} (- 2 x - h)

= - 2 x

続いて(2)です。3次関数ですが、やることは同じです。

f ´ (x) = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h}

= \lim_{h \to 0} \frac{{(x + h)}^{3} - x^{3}}{h}

= \lim_{h \to 0} \frac{3 x^{2} h + 3 x h^{2} + h^{3}}{h}

= \lim_{h \to 0} (3 x^{2} + 3 x h + h^{2})

= 3 x^{2}

今回の内容は以上です。実は圧倒的により便利な方法があるのですが、この微分の概念と基本的な定義は重要なので覚えておくといいと思います。

次回では、その便利な方法について解説します。(本当に作業量がまるで違います。)

問答庫塾
生徒募集中！

テーマカラー

文字サイズ